|
|
Application module:
Tessellated geometry |
ISO/TS 10303-1819:2021(E)
© ISO
|
This clause specifies the information requirements for the
Tessellated geometry
application module. The information requirements are specified as the
Application Reference Model (ARM) of this application module.
NOTE 1 A graphical representation of the information
requirements is given in
Annex C.
NOTE 2 The mapping specification is specified in
5.1. It shows how
the information requirements are met by using common resources and
constructs defined or imported in the MIM schema of this application
module.
This clause defines the information requirements to which implementations shall
conform using the EXPRESS language as defined in ISO 10303-11.
The following begins the
Tessellated_geometry_arm
schema and identifies the necessary external references.
EXPRESS specification:
*)
SCHEMA Tessellated_geometry_arm;
(*
The following EXPRESS interface statements specify the elements
imported from the ARMs of other application modules.
EXPRESS specification:
*)
USE FROM
Advanced_boundary_representation_arm;
--
ISO/TS 10303-1514
USE FROM
Basic_curve_arm;
--
ISO/TS 10303-1651
USE FROM
Basic_geometry_arm;
--
ISO/TS 10303-1652
USE FROM
Basic_geometric_topology_arm;
--
ISO/TS 10303-1323
USE FROM
Draughting_element_arm;
--
ISO/TS 10303-1310
USE FROM
Elemental_geometric_shape_arm;
--
ISO/TS 10303-1004
USE FROM
Elemental_topology_arm;
--
ISO/TS 10303-1005
REFERENCE FROM
Foundation_representation_arm
--
ISO/TS 10303-1006
(using_representations);
(*
NOTE 1
The schemas referenced above are specified in the following
part of ISO 10303:
| Advanced_boundary_representation_arm |
ISO/TS 10303-1514 |
| Basic_curve_arm |
ISO/TS 10303-1651 |
| Basic_geometry_arm |
ISO/TS 10303-1652 |
| Basic_geometric_topology_arm |
ISO/TS 10303-1323 |
| Draughting_element_arm |
ISO/TS 10303-1310 |
| Elemental_geometric_shape_arm |
ISO/TS 10303-1004 |
| Elemental_topology_arm |
ISO/TS 10303-1005 |
| Foundation_representation_arm |
ISO/TS 10303-1006 |
NOTE 2
See Annex C,
Figures
C.1, C.2, C.3, C.4and C.5
for a graphical representation of this schema.
This subclause specifies the ARM types
for this application module. The ARM types and
definitions are specified below.
An angular_deviation type specifies the maximum angular deviation of any facet in a tessellated shape model. Angular deviation is a measure of
the angle between the normal vectors at two points on a shape. The angular deviation for a given facet is the maximum angular
deviation for all pairs of points on the shape in the region being approximated by the facet.
NOTE
The angular deviation of a facet may be approximated by the maximum angular deviation between the pairs of vertex normals.
EXPRESS specification:
*)
TYPE
angular_deviation =
plane_angle_measure;
END_TYPE;
(*
A chordal_deviation type specifies the maximum chordal deviation of any facet in a tessellated shape model. Chordal deviation is the maximum
value of the minimum distance from any point on the edge of a facet to the closest point on the surface being approximated
by the facets.
EXPRESS specification:
*)
TYPE
chordal_deviation =
positive_length_measure;
END_TYPE;
(*
The edge_or_curve type allows for the designation of the data
types
Edge_curve and Curve.
This type identifies the entities which may be selected as the underlying geometry of a
Tessellated_edge.
EXPRESS specification:
*)
TYPE
edge_or_curve =
SELECT
(Edge_curve,
Curve);
END_TYPE;
(*
The face_or_surface type allows for the designation of the data
types
Face_surface and Surface.
This type identifies the entities which may be selected as the underlying geometry of a
Tessellated_face.
EXPRESS specification:
*)
TYPE
face_or_surface =
SELECT
(Face_surface,
Surface);
END_TYPE;
(*
A
length_to_height_ratio
type specifies the maximum ratio of height to length of any facets in a
tessellated shape model. The height is measured in a direction
perpendicular to the longest edge of a facet.
NOTE
length_to_height_ratio is a criterion used
to ensure reasonable proportions of the facets and thus, ensure the regularity of a set of facets in a tessellated geometry.
EXPRESS specification:
*)
TYPE
length_to_height_ratio =
ratio_measure;
END_TYPE;
(*
A maximum_edge_length type specifies the maximum length of any edge off any facet of a tessellated shape model.
EXPRESS specification:
*)
TYPE
maximum_edge_length =
positive_length_measure;
END_TYPE;
(*
The path_or_composite_curve type allows for the designation of the data
types
Path and Composite_curve.
This type identifies the entities in a geometric model which can be linked to a
Tessellated_wire.
EXPRESS specification:
*)
TYPE
path_or_composite_curve =
SELECT
(Path,
Composite_curve);
END_TYPE;
(*
A tessellated_facet_long_short_edge_ratio type specifies the maximum aspect ratio of any facet in a tessellated shape model.
A tessellated_facet_long_short_edge_ratio is the ratio of the longest to shortest edge of a facet.
NOTE
tessellated_facet_long_short_edge_ratio is an easily calculated
criterion used to verify that the individual facets in a tessellated geometry have edges of similar lengths.
EXPRESS specification:
*)
TYPE
tessellated_facet_long_short_edge_ratio =
ratio_measure;
END_TYPE;
(*
The tessellated_edge_or_vertex type allows for the designation of the data
types
Tessellated_edge and Tessellated_vertex.
This type identifies the entities that are used as items in the definition of a
Tessellated_wire.
EXPRESS specification:
*)
TYPE
tessellated_edge_or_vertex =
SELECT
(Tessellated_edge,
Tessellated_vertex);
END_TYPE;
(*
The tessellation_accuracy_parameter_item type is an
extensible list of alternate data types
that allows for the designation of the data
types angular_deviation, tessellated_facet_long_short_edge_ratio, chordal_deviation, length_to_height_ratio, and maximum_edge_length.
NOTE
The list of entity data types may be
extended in application modules that use the constructs of
this module.
A tessellation_accuracy_parameter_item
select type identifies the entities that are used as items
in the definition of tessellation_accuracy_parameters of a
Tessellated_shape_representation_with_accuracy_parameters.
EXPRESS specification:
*)
TYPE
tessellation_accuracy_parameter_item =
EXTENSIBLE
SELECT
(angular_deviation,
tessellated_facet_long_short_edge_ratio,
chordal_deviation,
length_to_height_ratio,
maximum_edge_length);
END_TYPE;
(*
The tg_draughting_callout_content_select type is an extension
of the
draughting_callout_content_select type.
It adds the data
type
Tessellated_annotation
to the list of alternate data types.
EXPRESS specification:
*)
TYPE
tg_draughting_callout_content_select =
SELECT
BASED_ON
draughting_callout_content_select
WITH
(Tessellated_annotation);
END_TYPE;
(*
This subclause specifies the ARM entities for this
module. Each ARM application entity is an atomic element that
embodies a unique application concept and contains attributes
specifying the data elements of the entity. The ARM
entities and definitions are specified below.
A Tessellated_annotation is a type of
Annotation_element
where the annotation geometry is provided as an
Tessellated_item.
EXPRESS specification:
*)
ENTITY Tessellated_annotation
SUBTYPE OF (Annotation_element);
SELF\Styled_element.element : Tessellated_item;
END_ENTITY;
(*
Attribute definitions:
element:
the
Tessellated_item
that is styled by the Tessellated_annotation.
A Tessellated_shape_representation is a type of
Geometric_model
in which the geometry is approximately represented by a tessellated model with planar facets.
EXPRESS specification:
*)
ENTITY Tessellated_shape_representation
SUBTYPE OF (Geometric_model);
WHERE
WR1: 'ELEMENTAL_GEOMETRIC_SHAPE_ARM.GEOMETRIC_COORDINATE_SPACE' IN TYPEOF(SELF\Representation.context_of_items);
WR2: NOT (SIZEOF(QUERY(it <* SELF.items | 'TESSELLATED_GEOMETRY_ARM.TESSELLATED_ITEM' IN TYPEOF(it))) = 0);
END_ENTITY;
(*
Formal propositions:
WR1:
The context of the Tessellated_shape_representation shall be a
Geometric_coordinate_space.
This ensures that the coordinates used to define the points of the tessellated geometry have defined units.
WR2:
The Tessellated_shape_representation shall shall contain at least 1 Tessellated_item in the items set.
A Tessellated_shape_representation_with_accuracy_parameters
is a type of Tessellated_shape_representation
which has additional parameters to define the accuracy of the tessellated approximation to the corresponding exact geometric
shape.
EXPRESS specification:
*)
ENTITY Tessellated_shape_representation_with_accuracy_parameters
SUBTYPE OF (Tessellated_shape_representation);
tessellation_accuracy_parameters : SET[1:?] OF tessellation_accuracy_parameter_item;
END_ENTITY;
(*
Attribute definitions:
tessellation_accuracy_parameters:
the set of parameters defining the accuracy of the Tessellated_shape_representation_with_accuracy_parameters.
A Tessellated_item is a type of
Detailed_geometric_model_element
used in the description of a tessellated shape.
A Tessellated_item is either a
Coordinates_list,
a
Tessellated_solid,
a
Tessellated_shell,
a
Tessellated_wire,
a
Tessellated_geometric_set,
a
Tessellated_curve_set,
a
Tessellated_point_set,
a
Tessellated_surface_set,
or a
Tessellated_structured_item.
EXPRESS specification:
*)
ENTITY Tessellated_item
ABSTRACT SUPERTYPE
OF (ONEOF (Coordinates_list,
Tessellated_solid,
Tessellated_shell,
Tessellated_wire,
Tessellated_geometric_set,
Tessellated_curve_set,
Tessellated_point_set,
Tessellated_surface_set,
Tessellated_structured_item))
SUBTYPE OF (Detailed_geometric_model_element);
WHERE
WR1: SIZEOF(QUERY(using_rep <* using_representations(SELF) | NOT ('TESSELLATED_GEOMETRY_ARM.TESSELLATED_SHAPE_REPRESENTATION'
IN TYPEOF(using_rep)))) = 0;
END_ENTITY;
(*
Formal propositions:
WR1:
A Tessellated_item shall only be used in a
Tessellated_shape_representation.
A Repositioned_tessellated_item is a type of
Tessellated_item
which has been re-postioned by defining the coordinates with respect to a new axis system.
EXPRESS specification:
*)
ENTITY Repositioned_tessellated_item
SUBTYPE OF (Tessellated_item);
location : Axis_placement_3d;
WHERE
WR1: NOT (SIZEOF(['TESSELLATED_GEOMETRY_ARM.TESSELLATED_CURVE_SET', 'TESSELLATED_GEOMETRY_ARM.TESSELLATED_GEOMETRIC_SET',
'TESSELLATED_GEOMETRY_ARM.TESSELLATED_POINT_SET', 'TESSELLATED_GEOMETRY_ARM.TESSELLATED_SURFACE_SET',
'TESSELLATED_GEOMETRY_ARM.TESSELLATED_SHELL', 'TESSELLATED_GEOMETRY_ARM.TESSELLATED_SOLID',
'TESSELLATED_GEOMETRY_ARM.TESSELLATED_WIRE'] * TYPEOF(SELF)) = 0);
END_ENTITY;
(*
Attribute definitions:
location:
an
Axis_placement_3d
defining the origin and axis direction for the coordinates of the referenced points in the Repositioned_tessellated_item.
Formal propositions:
WR1:
A Repositioned_tessellated_item shall only be used as a complex subtype with one of the following types of
Tessellated_item:
a Tessellated_curve_set,
a Tessellated_geometric_set,
a Tessellated_point_set,
a Tessellated_surface_set,
a Tessellated_shell,
a Tessellated_solid,
or a
Tessellated_wire.
A Tessellated_geometric_set is a type of
Tessellated_item
that is a collection of
Tessellated_items.
EXPRESS specification:
*)
ENTITY Tessellated_geometric_set
SUBTYPE OF (Tessellated_item);
children : SET[1:?] OF Tessellated_item;
END_ENTITY;
(*
Attribute definitions:
children:
the individual items of tessellated geometry.
A Tessellated_solid is a type of
Tessellated_item
that is a tessellated representation of a solid model.
Its geometry is defined as a set of
Tessellated_structured_items.
NOTE
The
Tessellated_structured_items
defining the geometry may be relocated in a local coordinate system by defining a complex instance of this entity with a
Repositioned_tessellated_item.
EXPRESS specification:
*)
ENTITY Tessellated_solid
SUBTYPE OF (Tessellated_item);
items : SET[1:?] OF Tessellated_structured_item;
geometric_link :
OPTIONAL
Manifold_solid_brep;
END_ENTITY;
(*
Attribute definitions:
items:
the set of
Tessellated_structured_items
defining the faces of the solid.
geometric_link:
a corresponding exact model of the solid.
The value of this attribute need not be specified.
A Tessellated_shell is a type of
Tessellated_item
that is a tessellated representation of a shell.
Its geometry is defined as a set of
Tessellated_structured_items.
NOTE
The
Tessellated_structured_items
defining the geometry may be relocated in a local coordinate system by defining a complex instance of this entity with a
Repositioned_tessellated_item.
EXPRESS specification:
*)
ENTITY Tessellated_shell
SUBTYPE OF (Tessellated_item);
items : SET[1:?] OF Tessellated_structured_item;
topological_link :
OPTIONAL
Connected_face_set;
END_ENTITY;
(*
Attribute definitions:
items:
the set of
Tessellated_structured_items
defining the faces of the shell.
topological_link:
a
Connected_face_set
representing the exact geometry of the shell.
The value of this attribute need not be specified.
A Tessellated_wire is a type of
Tessellated_item
that is a tessellated representation of a collection of bounded curves joined end to end.
Its geometry is defined as a set of tessellated edges and vertices.
NOTE
The edges and vertices defining the geometry may be relocated in a local coordinate system by defining
a complex instance of this entity with a
Repositioned_tessellated_item.
EXPRESS specification:
*)
ENTITY Tessellated_wire
SUBTYPE OF (Tessellated_item);
items : SET[1:?] OF tessellated_edge_or_vertex;
geometric_model_link :
OPTIONAL
path_or_composite_curve;
END_ENTITY;
(*
Attribute definitions:
items:
the set of
tessellated_edge_or_vertexs
defining the geometry of the wire.
geometric_model_link:
the corresponding exact geometry which may be a
path_or_composite_curve.
The value of this attribute need not be specified.
A Tessellated_curve_set is a type of
Tessellated_item
that is a tessellated representation of a collection of curves.
The geometry of each curve is defined as a list of points obtained via the line_strips attribute.
EXPRESS specification:
*)
ENTITY Tessellated_curve_set
SUBTYPE OF (Tessellated_item);
coordinates : Coordinates_list;
line_strips : LIST[1:?] OF LIST[2:?] OF INTEGER;
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
giving the coordinate values for points of the curves.
line_strips:
the list of lists of integers defining the locations in the coordinates list of the consecutive points for each curve.
A Tessellated_structured_item is a type of
Tessellated_item
which has a topological structure.
The links to topological components of an exact geometric model are defined with the subtypes.
A Tessellated_structured_item may be either a
Tessellated_face,
a
Tessellated_edge,
or a
Tessellated_vertex.
EXPRESS specification:
*)
ENTITY Tessellated_structured_item
SUPERTYPE OF (ONEOF (Tessellated_face,
Tessellated_edge,
Tessellated_vertex))
SUBTYPE OF (Tessellated_item);
END_ENTITY;
(*
A Tessellated_edge is a type of
Tessellated_structured_item.
The geometry of the Tessellated_edge is approximated by straight line segments joining the points listed.
NOTE 1
A Tessellated_edge may be used as the boundary between two
Tessellated_faces.
EXPRESS specification:
*)
ENTITY Tessellated_edge
SUPERTYPE OF (ONEOF (Tessellated_connecting_edge,
Cubic_bezier_tessellated_edge))
SUBTYPE OF (Tessellated_structured_item);
coordinates : Coordinates_list;
geometric_link :
OPTIONAL
edge_or_curve;
line_strip : LIST[2:?] OF INTEGER;
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
giving the coordinate values for points of the Tessellated_edge.
geometric_link:
the
edge_or_curve
of an exact model to which this Tessellated_edge corresponds.
The value of this attribute need not be specified.
line_strip:
the list of integers giving the locations in the coordinates list of consecutive points of this edge.
A Tessellated_connecting_edge is a type of
Tessellated_edge.
The Tessellated_connecting_edge connects two faces and contains information relating to the face normals.
EXPRESS specification:
*)
ENTITY Tessellated_connecting_edge
SUBTYPE OF (Tessellated_edge);
smooth : LOGICAL;
face1 : Tessellated_face;
face2 : Tessellated_face;
line_strip_face1 : LIST[2:?] OF INTEGER;
line_strip_face2 : LIST[2:?] OF INTEGER;
WHERE
WR1: SIZEOF(line_strip_face1) = SIZEOF(line_strip_face2);
WR2: SIZEOF(line_strip_face1) = SIZEOF(SELF\Tessellated_edge.line_strip);
END_ENTITY;
(*
Attribute definitions:
smooth:
a LOGICAL variable; if TRUE, there is tangent continuity where two faces join along this edge.
face1:
the first
Tessellated_face
using this edge.
face2:
the second
Tessellated_face
using this edge.
line_strip_face1:
the list of integers giving the locations in the normals list of face1 of the normals on the face1 side at consecutive points of this edge, and, for connection checking, if required, the locations in the face1 coordinates list or face1 pnindex of consecutive points of this edge; in cases where normals are not defined for face1
the locations in the coordinates list are given.
line_strip_face2:
the list of integers giving the locations in the normals list of face2 of the normals on the face2 side at consecutive points of this edge, and, for connection checking, if required, the locations in the face2 coordinates list or face2 pnindex of consecutive points of this edge; in cases where normals are not defined for face2
the locations in the coordinates list are given.
Formal propositions:
WR1:
The line_strip_face1 and line_strip_face2 shall be of the same size.
WR2:
The line_strip_face1 shall be of the same size as the inherited
line_strip
attribute.
A Cubic_bezier_tessellated_edge is a type of
Tessellated_edge which takes the form of a piecewise cubic bezier curve. The Cubic_bezier_tessellated_edge has its geometry defined by a list of control points, referenced by the inherited line_strip attribute; in this list only the points corresponding to ends of segments lie on the edge and the list of pointers is of
length 3n +1, where n is the number of segments.
EXPRESS specification:
*)
ENTITY Cubic_bezier_tessellated_edge
SUBTYPE OF (Tessellated_edge);
SELF\Tessellated_edge.line_strip : LIST[4:?] OF INTEGER;
END_ENTITY;
(*
Attribute definitions:
line_strip:
the list of 3n + 1 integers, where n is the number of cubic segments, giving the locations in the coordinates list of consecutive control points points of this edge.
A Cubic_tessellated_connecting_edge is a type of
Cubic_bezier_tessellated_edge which takes the form of a cubic curve and connects two Cubic_bezier_triangulated_faces. The Cubic_tessellated_connecting_edge has its geometry defined by a list of control points contained in the inherited line_strip attribute; in this list only the points corresponding to vertices of the cubic triangles of the adjacent faces lie on the
edge and the list of pointers is of length 3n +1, where n is the number of triangles with adjacent edges on each side of
the connecting edge.
EXPRESS specification:
*)
ENTITY Cubic_tessellated_connecting_edge
SUBTYPE OF (Cubic_bezier_tessellated_edge);
smooth : LOGICAL;
face1 : Cubic_bezier_triangulated_face;
face2 : Cubic_bezier_triangulated_face;
END_ENTITY;
(*
Attribute definitions:
smooth:
a LOGICAL variable; if TRUE, there is tangent continuity where two faces join along this edge;
face1:
the Cubic_bezier_triangulated_face to the left of this edge.
face2:
the Cubic_bezier_triangulated_face to the right of this edge.
A Tessellated_point_set is a type of
Tessellated_item
that is a collection of points used to define tessellated geometry.
EXPRESS specification:
*)
ENTITY Tessellated_point_set
SUBTYPE OF (Tessellated_item);
coordinates : Coordinates_list;
point_list : LIST[1:?] OF INTEGER;
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
giving the coordinate values for points of the set.
point_list:
the list of locations in the coordinates list of the individual points of this set.
A Tessellated_vertex is a type of
Tessellated_structured_item
and is a single vertex in a tessellated model.
EXPRESS specification:
*)
ENTITY Tessellated_vertex
SUBTYPE OF (Tessellated_structured_item);
coordinates : Coordinates_list;
topological_link :
OPTIONAL
Vertex_point;
point_index : INTEGER;
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
giving the vertex coordinate values.
topological_link:
an optional link to a topological
Vertex_point
entity.
The value of this attribute need not be specified.
point_index:
the location in the coordinates list of the coordinates for this vertex.
A Tessellated_surface_set is a type of
Tessellated_item
that is a tessellated representation of a collection of surfaces.
NOTE 1
If the surfaces are triangulated the geometry of the surfaces is fully defined by creating an instance of
one of the subtypes.
A Tessellated_surface_set is either a
Triangulated_surface_set
or a
Complex_triangulated_surface_set.
EXPRESS specification:
*)
ENTITY Tessellated_surface_set
ABSTRACT SUPERTYPE
OF (ONEOF (Triangulated_surface_set,
Complex_triangulated_surface_set))
SUBTYPE OF (Tessellated_item);
coordinates : Coordinates_list;
pnmax : INTEGER;
normals : LIST[0:?] OF LIST[3:3] OF REAL;
WHERE
WR1: ((SIZEOF(normals) = 0) OR (SIZEOF(normals) = 1) OR (SIZEOF(normals) = pnmax));
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
for the vertices of the triangles.
pnmax:
the larger of the number of points defined with the triangles or the number of unique point and
normal combinations in the set of triangles.
NOTE 2
In the case of a Tessellated_surface_set with a discontinuous boundary between faces it is possible to
have more than one normal defined at a point on the boundary.
normals:
the list of REAL triples defining the normals at the vertices of the triangles.
If the size of this list is greater than one the ordering of the normals is the same as the ordering used for the
pnindex.
Formal propositions:
WR1:
The size of normals shall be 0, 1 or equal to pnmax.
NOTE 3
If size = 0 normals are undefined at all vertices, if size = 1 the normal has the same value at each vertex
and the underlying surface is planar, if size is greater than 1 each triangle vertex has an individual underlying
surface normal defined.
A Triangulated_surface_set is a type of
Tessellated_surface_set
defining the geometry of the surface set as a set of triangles.
The individual triangles are defined by listing the coordinates of their vertices.
Normals to the surfaces defined by the set of triangles may be included.
EXPRESS specification:
*)
ENTITY Triangulated_surface_set
SUBTYPE OF (Tessellated_surface_set);
pnindex : LIST[0:?] OF INTEGER;
triangles : LIST[1:?] OF LIST[3:3] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\Tessellated_surface_set.pnmax));
WR2: NOT ((SIZEOF(pnindex) = 0) AND (SELF\Tessellated_surface_set.pnmax <> coordinates.npoints));
END_ENTITY;
(*
Attribute definitions:
pnindex:
the list of integers defining the locations in the coordinates list of the points and normals of the triangles.
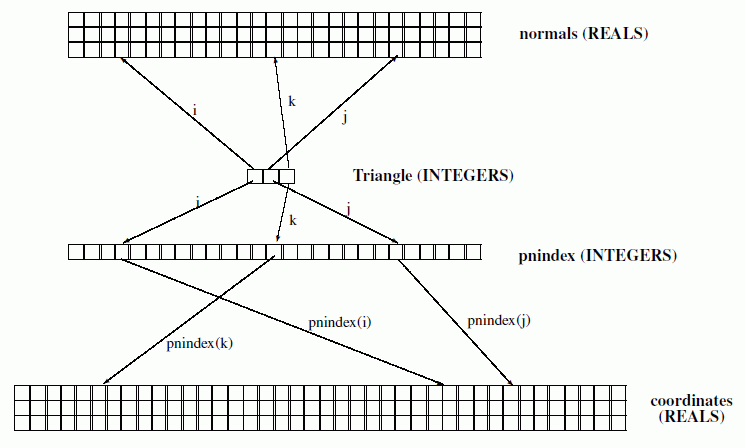
NOTE 1
See
Figure 2
for further details of use of pnindex.
triangles:
the list of INTEGER triples, in the range 1 to pnmax, giving the locations of the coordinate values in the
coordinates
list or pnindex for each triangle.
The ith triple in the list defines the orders in the appropriate list of the 3 vertices of the ith triangle.
NOTE 2
In the simplest case where no point is associated with more than 1 normal and the size of
coordinates
is
pnmax
the triangles refer directly to the
coordinates
list and pnindex is empty.
Formal propositions:
WR1:
The size of pnindex, if non-zero, shall be equal to
pnmax.
WR2:
The pnindex shall not be empty unless
pnmax
is equal to the size of the
coordinates
list.
NOTE 3
This option can only be used in the simple case of a local
Coordinates_list
and 0 or 1 normals per point.
A Complex_triangulated_surface_set is a type of
Tessellated_surface_set
defining the geometry by a set of triangles arranged in strips and fans.
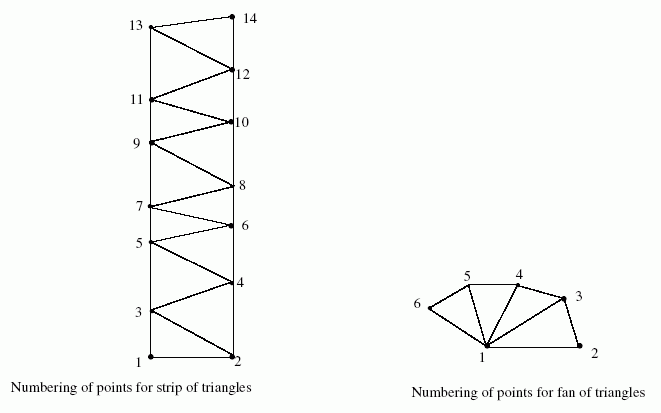
NOTE 1
The ordering of the points used to define the strips or fans of triangles is shown in
Figure 1.
EXPRESS specification:
*)
ENTITY Complex_triangulated_surface_set
SUBTYPE OF (Tessellated_surface_set);
pnindex : LIST[0:?] OF INTEGER;
triangle_strips : LIST[0:?] OF LIST[3:?] OF INTEGER;
triangle_fans : LIST[0:?] OF LIST[3:?] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\Tessellated_surface_set.pnmax));
WR2: NOT ((SIZEOF(pnindex) = 0) AND (SELF\Tessellated_surface_set.pnmax <> coordinates.npoints));
WR3: NOT ((SIZEOF(triangle_strips) = 0) AND (SIZEOF(triangle_fans) = 0));
END_ENTITY;
(*
Attribute definitions:
pnindex:
the list of integers defining the locations in the
coordinates
list of the points and normals of the triangles.
triangle_strips:
the list of lists of INTEGERs giving the locations of the coordinate values in the
coordinates
list for each strip of triangles.
Each sublist defines the orders in the
coordinates
list, via the pnindex if used, of the vertices of the ith strip of triangles.
NOTE 2
If required a single triangle can be included in this structure as a strip of one triangle, in which case the
sublist will contain 3 INTEGERs.
triangle_fans:
the list of lists of INTEGERs giving the locations of the coordinate values in the
coordinates
list for each fan of triangles.
Each sublist defines the orders in the
coordinates
list of the vertices of the ith fan of triangles.
NOTE 3
In the simplest case where no point is associated with more than 1 normal and the size of
coordinates
is
pnmax
the triangles defined by the strips and fans refer directly to the
coordinates
list and pnindex is empty.
Formal propositions:
WR1:
The size of pnindex, if non-zero, shall be equal to
pnmax.
WR2:
The pnindex shall not be empty unless
pnmax
is equal to the size of the
coordinates
list.
NOTE 4
This option can only be used in the simple case of a local
Coordinates_list
and 0 or 1 normals per point.
WR3:
The triangle_strips list and the triangle_fans list shall not both be empty.
A Tessellated_face is a type of
Tessellated_structured_item
that represents a face of a tessellated model.
A Tessellated_face is either a
Triangulated_face
or a
Complex_triangulated_face.
EXPRESS specification:
*)
ENTITY Tessellated_face
ABSTRACT SUPERTYPE
OF (ONEOF (Triangulated_face,
Complex_triangulated_face,
Cubic_bezier_triangulated_face))
SUBTYPE OF (Tessellated_structured_item);
coordinates : Coordinates_list;
pnmax : INTEGER;
normals : LIST[0:?] OF LIST[3:3] OF REAL;
geometric_link :
OPTIONAL
face_or_surface;
WHERE
WR1: ((SIZEOF(normals) = 0) OR (SIZEOF(normals) = 1) OR (SIZEOF(normals) = pnmax));
END_ENTITY;
(*
Attribute definitions:
coordinates:
the
Coordinates_list
for the points of the face.
pnmax:
the larger of the number of points defined with the face or the number of unique point and normal combinations in the face.
normals:
the list of REAL triples defining the normals at the points of the face.
If the size of this list is greater than one the ordering of the normals is the same as the ordering used for the points
via
pnindex in one of the subtypes.
geometric_link:
the face or surface of an exact model to which this Tessellated_face corresponds.
The value of this attribute need not be specified.
Formal propositions:
WR1:
The size of normals shall be 0, 1 or equal to pnmax.
NOTE
If size = 0 normals are undefined at all face points, if size = 1 the normal has the same value at each
face point and the underlying surface is planar, if size is greater than 1 each point on the face has an individual
underlying surface normal defined.
A Triangulated_face is a type of
Tessellated_face
that has its geometry defined by a set of triangles.
EXPRESS specification:
*)
ENTITY Triangulated_face
SUBTYPE OF (Tessellated_face);
pnindex : LIST[0:?] OF INTEGER;
triangles : LIST[1:?] OF LIST[3:3] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\Tessellated_face.pnmax));
WR2: NOT ((SIZEOF(pnindex) = 0) AND (SELF\Tessellated_face.pnmax <> coordinates.npoints));
END_ENTITY;
(*
Attribute definitions:
pnindex:
the list of integers defining the locations in the
coordinates
list of the points and normals of the triangles of the face.
triangles:
the list of INTEGER triples, in the range 1 to
pnmax,
giving the locations of the coordinate values in the
coordinates
list or in pnindex for each triangle.
The ith triple in the list defines the orders in the appropriate list of the 3 vertices of the ith triangle.
NOTE 1
See
Figure 2
for further details of use of pnindex.
Figure 2 — Use of pnindex to locate coordinates
NOTE 2
In the simplest case where no point is associated with more than 1 normal and the size of
coordinates
is
pnmax
the triangles refer directly to the
coordinates
list and pnindex is empty.
In all other cases pnindex is required to identify points and normals for the triangles.
Formal propositions:
WR1:
The size of pnindex, if non-zero, shall be equal to
pnmax.
WR2:
The pnindex shall not be empty unless
pnmax
is equal to the size of the
coordinates
list.
NOTE 3
This option can only be used in the simple case of a local
Coordinates_list
and 0 or 1 normals per point.
A Complex_triangulated_face is a type of
Tessellated_face
defining the geometry as a set of triangles arranged in strips and fans.
NOTE 1
The ordering of the points used to define the strips or fans of triangles is shown in
Figure 1.
Figure 1 — Ordering of points for Complex_triangulated_face
EXPRESS specification:
*)
ENTITY Complex_triangulated_face
SUBTYPE OF (Tessellated_face);
pnindex : LIST[0:?] OF INTEGER;
triangle_strips : LIST[0:?] OF LIST[3:?] OF INTEGER;
triangle_fans : LIST[0:?] OF LIST[3:?] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\Tessellated_face.pnmax));
WR2: NOT ((SIZEOF(pnindex) = 0) AND (SELF\Tessellated_face.pnmax <> coordinates.npoints));
WR3: NOT ((SIZEOF(triangle_strips) = 0) AND (SIZEOF(triangle_fans) = 0));
END_ENTITY;
(*
Attribute definitions:
pnindex:
the list of integers defining the locations in the
coordinates
list of the points and normals of the triangles.
triangle_strips:
the list of lists of INTEGERs giving the locations of the coordinate values in the
coordinates
list for each strip of triangles.
Each sublist defines the orders in the
coordinates
list, via the pnindex if used, of the vertices of the ith strip of triangles.
NOTE 2
If required a single triangle can be included in this structure as a strip of one triangle, in which case the
sublist will contain 3 INTEGERs.
triangle_fans:
the list of lists of INTEGERs giving the locations of the coordinate values in the
coordinates
list for each fan of triangles.
Each sublist defines the orders in the
coordinates
list of the vertices of the ith fan of triangles.
NOTE 3
In the simplest case where no point is associated with more than 1 normal and the size of
coordinates
is
pnmax
the triangles defined by the strips and fans refer directly to the
coordinates
list and pnindex is empty.
In all other cases pnindex is required to identify points and normals for the triangles.
Formal propositions:
WR1:
The size of pnindex, if non-zero, shall be equal to
pnmax.
WR2:
The pnindex shall not be empty unless
pnmax
is equal to the size of the
coordinates
list.
NOTE 4
This option can only be used in the simple case of a local
Coordinates_list
and 0 or 1 normals per point.
WR3:
The triangle_strips list and the triangle_fans list shall not both be empty.
A Cubic_bezier_triangulated_face is a type of
Tessellated_face that has its geometry defined by a set of curved triangles. Each of the triangles is a 3 sided Bezier cubic surface defined
by a list of 10 control points, 9 near the edges and one above the centre. The control points P1 , P2 , P3 , are at the vertices of the triangle. Each triangle is a bi-parametric surface with equation:
s(u,v) = (1 - u -v)3P1 + u3P2 + v3P3 + 3(1 - u -v)2uP4 + 3(1 - u -v)u2P5 + 3u2vP6 + 3uv2P7 + 3(1 - u -v)v2P8 + 3(1 - u -v)2vP9 + 6uv(1 - u -v)P10
The parametric range for each triangle is 0 ≤ u ≤ 1; 0 ≤ v ≤ 1; with u + v ≤ 1.
At each vertex the tangent along the edge of the triangle is in the direction of the next conrol point along this edge and
has a magnnitude equal to 3 times this distance. At vertex P1 the tangent vector along the edge u = 0 is t = 3(P4 -P1), other tangent vectors are defined in a similar way.
Continuity of geometry between adjacent triangles is assured provided the adjacent edges reference the same 4 control points.
Each edge of the triangle is a Bezier cubic curve of parametric length 1 defined by the 4 control points along that edge.
P1, P4, P5, P2 define the cubic curve of the first edge of the triangle, other edges are defined in a similar manner.
Figure 3 — Relationship between control points and triangular surface
NOTE 1
See Figure (3) for illustration of the numbering of the control points.
EXPRESS specification:
*)
ENTITY Cubic_bezier_triangulated_face
SUBTYPE OF (Tessellated_face);
ctriangles : LIST[1:?] OF LIST[10:10] OF INTEGER;
WHERE
WR1: SIZEOF(SELF\Tessellated_face.normals) = 0;
END_ENTITY;
(*
Attribute definitions:
ctriangles:
the list of list of 10 INTEGER pointers, giving the locations of the coordinate values of the control points for each triangle
in the coordinates list.
NOTE 2
The control points for each triangle are ordered as shown in Figure (3)
Formal propositions:
WR1:
The size of normals list. shall be zero, the geometry of each triangle is completely defined by the control points.
A Coordinates_list is a type of
Tessellated_item
that defines the coordinate values for points used in a
Tessellated_shape_representation.
EXPRESS specification:
*)
ENTITY Coordinates_list
SUBTYPE OF (Tessellated_item);
npoints : INTEGER;
position_coords : LIST[1:?] OF LIST[3:3] OF REAL;
WHERE
WR1: npoints = SIZEOF(position_coords);
WR2: SIZEOF(['TESSELLATED_GEOMETRY_ARM.REPOSITIONED_TESSELLATED_ITEM'] * TYPEOF(SELF)) = 0;
END_ENTITY;
(*
Attribute definitions:
npoints:
the number of points with coordinates in the list.
position_coords:
the list of real triples defining the coordinates of the points.
NOTE 1
These real triples have the semantics of
length measures,
but are not formally defined as such, the units for these are defined since a
Tessellated_item
is required to be used in a
Tessellated_shape_representation
having a
Geometric_coordinate_space.
Formal propositions:
WR1:
The value of npoints shall be equal to the size of the position_coords list.
WR2:
This entity shall not be instantiated as a complex subtype with
Repositioned_tessellated_item.
NOTE 2
This rule together with the ONEOF rule on the supertype
Tessellated_item
ensures that it is not instantiated with any subtype of
Tessellated_item.
*)
END_SCHEMA; -- Tessellated_geometry_arm
(*
© ISO 2021 — All rights reserved